Which Quadrilaterals Have Perpendicular Diagonals

Polygon with iv sides and four corners

Quadrilateral
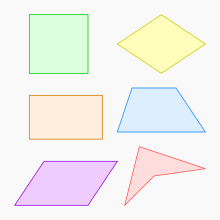Some types of quadrilaterals
Edges and vertices	4
Schläfli symbol	{four} (for square)
Expanse	various methods; come across below
Internal angle (degrees)	ninety° (for square and rectangle)

In geometry a quadrilateral is a iv-sided polygon, having 4 edges (sides) and iv corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, significant "side". It is also called a tetragon, derived from greek "tetra" significant "iv" and "gon" significant "corner" or "bending", in analogy to other polygons (e.g. pentagon). Since "gon" ways "angle", it is analogously chosen a quadrangle, or 4-angle. A quadrilateral with vertices ${\displaystyle A}$ , ${\displaystyle B}$ , ${\displaystyle C}$ and ${\displaystyle D}$ is sometimes denoted as ${\displaystyle \square ABCD}$ .^[1]

Quadrilaterals are either elementary (not cocky-intersecting), or complex (cocky-intersecting, or crossed). Unproblematic quadrilaterals are either convex or concave.

The interior angles of a simple (and planar) quadrilateral ABCD add upwardly to 360 degrees of arc, that is^[1]

${\displaystyle \angle A+\angle B+\bending C+\angle D=360^{\circ }.}$

This is a special case of the n-gon interior angle sum formula: Due south = (n − two) × 180°.^[two]

All non-self-crossing quadrilaterals tile the plane, by repeated rotation effectually the midpoints of their edges.^[three]

Simple quadrilaterals [edit]

Any quadrilateral that is not self-intersecting is a unproblematic quadrilateral.

Convex quadrilateral [edit]

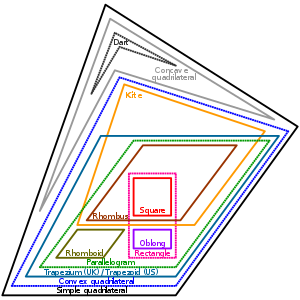
Euler diagram of some types of simple quadrilaterals. (UK) denotes British English language and (Usa) denotes American English.

Convex quadrilaterals by symmetry, represented with a Hasse diagram.

In a convex quadrilateral all interior angles are less than 180°, and the two diagonals both lie inside the quadrilateral.

• Irregular quadrilateral (British English language) or trapezium (North American English): no sides are parallel. (In British English, this was once chosen a trapezoid. For more than, run into Trapezoid § Trapezium vs Trapezoid)
• Trapezium (United kingdom of great britain and northern ireland) or trapezoid (US): at to the lowest degree one pair of reverse sides are parallel. Trapezia (United kingdom) and trapezoids (US) include parallelograms.
• Isosceles trapezium (UK) or isosceles trapezoid (US): one pair of contrary sides are parallel and the base of operations angles are equal in mensurate. Culling definitions are a quadrilateral with an axis of symmetry bisecting i pair of opposite sides, or a trapezoid with diagonals of equal length.
• Parallelogram: a quadrilateral with two pairs of parallel sides. Equivalent atmospheric condition are that opposite sides are of equal length; that reverse angles are equal; or that the diagonals bisect each other. Parallelograms include rhombi (including those rectangles chosen squares) and rhomboids (including those rectangles called oblongs). In other words, parallelograms include all rhombi and all rhomboids, and thus as well include all rectangles.
• Rhombus, rhomb:^[ane] all four sides are of equal length (equilateral). An equivalent condition is that the diagonals perpendicularly bifurcate each other. Informally: "a pushed-over square" (but strictly including a square, too).
• Rhomboid: a parallelogram in which adjacent sides are of unequal lengths, and some angles are oblique (equiv., having no correct angles). Informally: "a pushed-over ellipsoidal". Not all references agree, some define a rhomboid every bit a parallelogram that is non a rhombus.^[4]
• Rectangle: all iv angles are correct angles (equiangular). An equivalent condition is that the diagonals bisect each other, and are equal in length. Rectangles include squares and oblongs. Informally: "a box or oblong" (including a square).
• Foursquare (regular quadrilateral): all iv sides are of equal length (equilateral), and all four angles are correct angles. An equivalent condition is that opposite sides are parallel (a foursquare is a parallelogram), and that the diagonals perpendicularly bisect each other and are of equal length. A quadrilateral is a square if and merely if it is both a rhombus and a rectangle (i.e., four equal sides and four equal angles).
• Ellipsoidal: longer than wide, or wider than long (i.due east., a rectangle that is not a square).^[five]
• Kite: ii pairs of next sides are of equal length. This implies that one diagonal divides the kite into congruent triangles, and so the angles betwixt the two pairs of equal sides are equal in mensurate. Information technology also implies that the diagonals are perpendicular. Kites include rhombi.

• Tangential quadrilateral: the 4 sides are tangents to an inscribed circle. A convex quadrilateral is tangential if and only if opposite sides have equal sums.
• Tangential trapezoid: a trapezoid where the four sides are tangents to an inscribed circle.
• Cyclic quadrilateral: the four vertices lie on a circumscribed circle. A convex quadrilateral is circadian if and only if opposite angles sum to 180°.
• Right kite: a kite with two opposite right angles. It is a type of cyclic quadrilateral.
• Harmonic quadrilateral: the products of the lengths of the opposing sides are equal. It is a type of circadian quadrilateral.
• Bicentric quadrilateral: it is both tangential and cyclic.
• Orthodiagonal quadrilateral: the diagonals cross at correct angles.
• Equidiagonal quadrilateral: the diagonals are of equal length.
• Ex-tangential quadrilateral: the four extensions of the sides are tangent to an excircle.
• An equilic quadrilateral has two contrary equal sides that when extended, run into at sixty°.
• A Watt quadrilateral is a quadrilateral with a pair of opposite sides of equal length.^[6]
• A quadric quadrilateral is a convex quadrilateral whose four vertices all lie on the perimeter of a square.^[7]
• A diametric quadrilateral is a circadian quadrilateral having i of its sides as a diameter of the circumcircle.^[8]
• A Hjelmslev quadrilateral is a quadrilateral with 2 right angles at contrary vertices.^[ix]

Concave quadrilaterals [edit]

In a concave quadrilateral, 1 interior bending is bigger than 180°, and one of the ii diagonals lies outside the quadrilateral.

• A dart (or arrowhead) is a concave quadrilateral with bilateral symmetry similar a kite, but where one interior bending is reflex. Encounter Kite.

Circuitous quadrilaterals [edit]

A self-intersecting quadrilateral is chosen variously a cross-quadrilateral, crossed quadrilateral, butterfly quadrilateral or bow-tie quadrilateral. In a crossed quadrilateral, the 4 "interior" angles on either side of the crossing (two acute and two reflex, all on the left or all on the correct equally the figure is traced out) add upwards to 720°.^[10]

• Crossed trapezoid (US) or trapezium (Commonwealth):^[eleven] a crossed quadrilateral in which one pair of nonadjacent sides is parallel (like a trapezoid)
• Antiparallelogram: a crossed quadrilateral in which each pair of nonadjacent sides have equal lengths (like a parallelogram)
• Crossed rectangle: an antiparallelogram whose sides are two reverse sides and the two diagonals of a rectangle, hence having one pair of parallel opposite sides
• Crossed foursquare: a special example of a crossed rectangle where two of the sides intersect at right angles

Special line segments [edit]

The two diagonals of a convex quadrilateral are the line segments that connect opposite vertices.

The two bimedians of a convex quadrilateral are the line segments that connect the midpoints of opposite sides.^[12] They intersect at the "vertex centroid" of the quadrilateral (see § Remarkable points and lines in a convex quadrilateral below).

The 4 maltitudes of a convex quadrilateral are the perpendiculars to a side—through the midpoint of the opposite side.^[13]

Expanse of a convex quadrilateral [edit]

In that location are diverse general formulas for the area K of a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD and d = DA .

Trigonometric formulas [edit]

The expanse can be expressed in trigonometric terms as^[14]

${\displaystyle K={\frac {pq}{ii}}\sin \theta ,}$

where the lengths of the diagonals are p and q and the bending between them is θ .^[xv] In the case of an orthodiagonal quadrilateral (e.thou. rhombus, square, and kite), this formula reduces to ${\displaystyle K={\tfrac {pq}{2}}}$ since θ is 90°.

The area tin can be likewise expressed in terms of bimedians every bit^[16]

${\displaystyle K=mn\sin \varphi ,}$

where the lengths of the bimedians are thousand and n and the angle between them is φ .

Bretschneider's formula^{[17] [14]} expresses the area in terms of the sides and ii opposite angles:

${\displaystyle {\begin{aligned}M&={\sqrt {(southward-a)(s-b)(due south-c)(south-d)-{\tfrac {1}{two}}abcd\;[ane+\cos(A+C)]}}\\&={\sqrt {(s-a)(s-b)(s-c)(due south-d)-abcd\left[\cos ^{2}\left({\frac {A+C}{2}}\right)\right]}}\end{aligned}}}$

where the sides in sequence are a , b , c , d , where s is the semiperimeter, and A and C are two (in fact, any 2) opposite angles. This reduces to Brahmagupta'southward formula for the area of a cyclic quadrilateral—when A + C = 180° .

Another area formula in terms of the sides and angles, with bending C being between sides b and c , and A beingness betwixt sides a and d , is

${\displaystyle K={\frac {advertizing}{2}}\sin {A}+{\frac {bc}{ii}}\sin {C}.}$

In the example of a cyclic quadrilateral, the latter formula becomes ${\displaystyle One thousand={\frac {advertisement+bc}{two}}\sin {A}.}$

In a parallelogram, where both pairs of opposite sides and angles are equal, this formula reduces to ${\displaystyle K=ab\cdot \sin {A}.}$

Alternatively, nosotros tin write the area in terms of the sides and the intersection angle θ of the diagonals, every bit long θ is not 90°:^[xviii]

${\displaystyle Thousand={\frac {\left|\tan \theta \right|}{iv}}\cdot \left|a^{two}+c^{two}-b^{2}-d^{2}\right|.}$

In the case of a parallelogram, the latter formula becomes ${\displaystyle K={\frac {\left|\tan \theta \right|}{two}}\cdot \left|a^{2}-b^{ii}\right|.}$

Another area formula including the sides a , b , c , d is^[xvi]

${\displaystyle K={\frac {\sqrt {((a^{two}+c^{2})-2x^{two})((b^{2}+d^{ii})-2x^{ii})}}{2}}\sin {\varphi }}$

where 10 is the distance between the midpoints of the diagonals, and φ is the angle between the bimedians.

The last trigonometric area formula including the sides a , b , c , d and the bending α (between a and b ) is:^[nineteen]

${\displaystyle Yard={\frac {ab}{ii}}\sin {\alpha }+{\frac {\sqrt {4c^{2}d^{two}-(c^{2}+d^{2}-a^{2}-b^{2}+2ab\cdot \cos {\alpha })^{ii}}}{iv}},}$

which can also be used for the area of a concave quadrilateral (having the concave role opposite to bending α ), by just changing the beginning sign + to -.

Not-trigonometric formulas [edit]

The following two formulas express the area in terms of the sides a , b , c and d , the semiperimeter due south , and the diagonals p , q :

${\displaystyle One thousand={\sqrt {(south-a)(s-b)(south-c)(s-d)-{\tfrac {1}{4}}(ac+bd+pq)(ac+bd-pq)}},}$ ^[20]

${\displaystyle K={\frac {\sqrt {4p^{2}q^{2}-\left(a^{2}+c^{2}-b^{2}-d^{two}\correct)^{two}}}{4}}.}$ ^[21]

The first reduces to Brahmagupta's formula in the cyclic quadrilateral case, since then pq = ac + bd .

The area can also be expressed in terms of the bimedians m , n and the diagonals p , q :

${\displaystyle K={\frac {\sqrt {(grand+n+p)(m+north-p)(m+n+q)(m+north-q)}}{ii}},}$ ^[22]

${\displaystyle Yard={\frac {\sqrt {p^{2}q^{2}-(m^{2}-n^{2})^{2}}}{2}}.}$ ^{[23] : Thm. 7}

In fact, whatsoever three of the 4 values 1000 , northward , p , and q suffice for decision of the area, since in whatsoever quadrilateral the four values are related by ${\displaystyle p^{2}+q^{2}=2(m^{2}+n^{two}).}$ ^{[24] : p. 126} The corresponding expressions are:^[25]

${\displaystyle Yard={\frac {\sqrt {[(m+n)^{2}-p^{2}]\cdot [p^{2}-(1000-n)^{two}]}}{two}},}$

if the lengths of two bimedians and 1 diagonal are given, and^[25]

${\displaystyle Yard={\frac {\sqrt {[(p+q)^{ii}-4m^{2}]\cdot [4m^{2}-(p-q)^{2}]}}{4}},}$

if the lengths of ii diagonals and one bimedian are given.

Vector formulas [edit]

The area of a quadrilateral ABCD can be calculated using vectors. Let vectors AC and BD form the diagonals from A to C and from B to D . The area of the quadrilateral is then

${\displaystyle K={\frac {|\mathbf {Ac} \times \mathbf {BD} |}{2}},}$

which is half the magnitude of the cantankerous product of vectors AC and BD . In 2-dimensional Euclidean space, expressing vector Air-conditioning every bit a free vector in Cartesian infinite equal to ( x ₁,y ₁ ) and BD as ( ten _two,y ₂ ), this tin can be rewritten as:

${\displaystyle Thou={\frac {|x_{1}y_{two}-x_{two}y_{i}|}{2}}.}$

Diagonals [edit]

Properties of the diagonals in quadrilaterals [edit]

In the following table it is listed if the diagonals in some of the most bones quadrilaterals bisect each other, if their diagonals are perpendicular, and if their diagonals accept equal length.^[26] The listing applies to the most general cases, and excludes named subsets.

Quadrilateral	Bisecting diagonals	Perpendicular diagonals	Equal diagonals
Trapezoid	No	See annotation ane	No
Isosceles trapezoid	No	Meet annotation 1	Yes
Parallelogram	Yep	No	No
Kite	See note ii	Yes	See note 2
Rectangle	Yes	No	Yes
Rhombus	Yeah	Yes	No
Foursquare	Yes	Yep	Yes

Note 1: The most full general trapezoids and isosceles trapezoids do non take perpendicular diagonals, merely there are infinite numbers of (non-similar) trapezoids and isosceles trapezoids that do have perpendicular diagonals and are not whatsoever other named quadrilateral.

Annotation two: In a kite, ane diagonal bisects the other. The most general kite has unequal diagonals, but there is an infinite number of (not-similar) kites in which the diagonals are equal in length (and the kites are not any other named quadrilateral).

Lengths of the diagonals [edit]

The lengths of the diagonals in a convex quadrilateral ABCD tin can be calculated using the law of cosines on each triangle formed past one diagonal and two sides of the quadrilateral. Thus

${\displaystyle p={\sqrt {a^{two}+b^{2}-2ab\cos {B}}}={\sqrt {c^{2}+d^{2}-2cd\cos {D}}}}$

and

${\displaystyle q={\sqrt {a^{2}+d^{2}-2ad\cos {A}}}={\sqrt {b^{2}+c^{two}-2bc\cos {C}}}.}$

Other, more symmetric formulas for the lengths of the diagonals, are^[27]

${\displaystyle p={\sqrt {\frac {(air-conditioning+bd)(advertizing+bc)-2abcd(\cos {B}+\cos {D})}{ab+cd}}}}$

and

${\displaystyle q={\sqrt {\frac {(ab+cd)(ac+bd)-2abcd(\cos {A}+\cos {C})}{ad+bc}}}.}$

Generalizations of the parallelogram law and Ptolemy's theorem [edit]

In whatsoever convex quadrilateral ABCD, the sum of the squares of the four sides is equal to the sum of the squares of the two diagonals plus 4 times the foursquare of the line segment connecting the midpoints of the diagonals. Thus

${\displaystyle a^{two}+b^{2}+c^{2}+d^{2}=p^{2}+q^{2}+4x^{ii}}$

where 10 is the distance between the midpoints of the diagonals.^{[24] : p.126} This is sometimes known every bit Euler's quadrilateral theorem and is a generalization of the parallelogram constabulary.

The German mathematician Carl Anton Bretschneider derived in 1842 the post-obit generalization of Ptolemy's theorem, regarding the production of the diagonals in a convex quadrilateral^[28]

${\displaystyle p^{2}q^{two}=a^{2}c^{2}+b^{2}d^{2}-2abcd\cos {(A+C)}.}$

This relation can exist considered to be a law of cosines for a quadrilateral. In a cyclic quadrilateral, where A + C = 180°, it reduces to pq = air conditioning + bd. Since cos (A + C) ≥ −i, it also gives a proof of Ptolemy's inequality.

Other metric relations [edit]

If X and Y are the feet of the normals from B and D to the diagonal AC = p in a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD, d = DA, so^{[29] : p.14}

${\displaystyle XY={\frac {|a^{2}+c^{2}-b^{2}-d^{ii}|}{2p}}.}$

In a convex quadrilateral ABCD with sides a = AB, b = BC, c = CD, d = DA, and where the diagonals intersect at E,

${\displaystyle efgh(a+c+b+d)(a+c-b-d)=(agh+cef+beh+dfg)(agh+cef-beh-dfg)}$

where e = AE, f = BE, k = CE, and h = DE.^[30]

The shape and size of a convex quadrilateral are fully adamant by the lengths of its sides in sequence and of ane diagonal between ii specified vertices. The ii diagonals p, q and the four side lengths a, b, c, d of a quadrilateral are related^[14] past the Cayley-Menger determinant, as follows:

${\displaystyle \det {\begin{bmatrix}0&a^{2}&p^{two}&d^{two}&1\\a^{2}&0&b^{2}&q^{2}&1\\p^{2}&b^{2}&0&c^{ii}&ane\\d^{ii}&q^{ii}&c^{two}&0&i\\1&ane&1&ane&0\cease{bmatrix}}=0.}$

Angle bisectors [edit]

The internal angle bisectors of a convex quadrilateral either course a cyclic quadrilateral^{[24] : p.127} (that is, the iv intersection points of next angle bisectors are concyclic) or they are concurrent. In the latter case the quadrilateral is a tangential quadrilateral.

In quadrilateral ABCD, if the angle bisectors of A and C meet on diagonal BD, then the angle bisectors of B and D meet on diagonal AC.^[31]

Bimedians [edit]

The Varignon parallelogram EFGH

The bimedians of a quadrilateral are the line segments connecting the midpoints of the opposite sides. The intersection of the bimedians is the centroid of the vertices of the quadrilateral.^[fourteen]

The midpoints of the sides of whatever quadrilateral (convex, concave or crossed) are the vertices of a parallelogram chosen the Varignon parallelogram. It has the post-obit properties:

• Each pair of contrary sides of the Varignon parallelogram are parallel to a diagonal in the original quadrilateral.
• A side of the Varignon parallelogram is one-half as long as the diagonal in the original quadrilateral it is parallel to.
• The area of the Varignon parallelogram equals one-half the surface area of the original quadrilateral. This is true in convex, concave and crossed quadrilaterals provided the area of the latter is defined to be the difference of the areas of the two triangles it is composed of.^[32]
• The perimeter of the Varignon parallelogram equals the sum of the diagonals of the original quadrilateral.
• The diagonals of the Varignon parallelogram are the bimedians of the original quadrilateral.

The two bimedians in a quadrilateral and the line segment joining the midpoints of the diagonals in that quadrilateral are concurrent and are all bisected by their indicate of intersection.^{[24] : p.125}

In a convex quadrilateral with sides a, b, c and d, the length of the bimedian that connects the midpoints of the sides a and c is

${\displaystyle one thousand={\tfrac {1}{two}}{\sqrt {-a^{ii}+b^{two}-c^{2}+d^{two}+p^{2}+q^{2}}}}$

where p and q are the length of the diagonals.^[33] The length of the bimedian that connects the midpoints of the sides b and d is

${\displaystyle n={\tfrac {1}{2}}{\sqrt {a^{2}-b^{2}+c^{two}-d^{ii}+p^{2}+q^{2}}}.}$

Hence^{[24] : p.126}

${\displaystyle \displaystyle p^{2}+q^{two}=two(m^{2}+n^{2}).}$

This is also a corollary to the parallelogram police practical in the Varignon parallelogram.

The lengths of the bimedians can also exist expressed in terms of 2 opposite sides and the distance x between the midpoints of the diagonals. This is possible when using Euler's quadrilateral theorem in the above formulas. Whence^[23]

${\displaystyle m={\tfrac {ane}{two}}{\sqrt {2(b^{2}+d^{2})-4x^{2}}}}$

and

${\displaystyle n={\tfrac {one}{2}}{\sqrt {2(a^{2}+c^{2})-4x^{2}}}.}$

Note that the ii opposite sides in these formulas are not the two that the bimedian connects.

In a convex quadrilateral, at that place is the following dual connexion between the bimedians and the diagonals:^[29]

• The two bimedians have equal length if and only if the 2 diagonals are perpendicular.
• The 2 bimedians are perpendicular if and but if the two diagonals have equal length.

Trigonometric identities [edit]

The four angles of a elementary quadrilateral ABCD satisfy the following identities:^[34]

${\displaystyle \sin {A}+\sin {B}+\sin {C}+\sin {D}=4\sin {\frac {A+B}{two}}\sin {\frac {A+C}{2}}\sin {\frac {A+D}{2}}}$

and

${\displaystyle {\frac {\tan {A}\tan {B}-\tan {C}\tan {D}}{\tan {A}\tan {C}-\tan {B}\tan {D}}}={\frac {\tan {(A+C)}}{\tan {(A+B)}}}.}$

Also,^[35]

${\displaystyle {\frac {\tan {A}+\tan {B}+\tan {C}+\tan {D}}{\cot {A}+\cot {B}+\cot {C}+\cot {D}}}=\tan {A}\tan {B}\tan {C}\tan {D}.}$

In the last two formulas, no angle is allowed to be a correct bending, since tan 90° is not divers.

Let ${\displaystyle a}$ , ${\displaystyle b}$ , ${\displaystyle c}$ , ${\displaystyle d}$ be the sides of a convex quadrilateral, ${\displaystyle s}$ is the semiperimeter, and ${\displaystyle A}$ and ${\displaystyle C}$ are reverse angles, and then^[36]

${\displaystyle ad\sin ^{2}{\frac {A}{2}}+bc\cos ^{2}{\frac {C}{2}}=(s-a)(s-d)}$

and

${\displaystyle bc\sin ^{2}{\frac {C}{2}}+ad\cos ^{two}{\frac {A}{two}}=(s-b)(s-c)}$ .

We tin can employ these identities to derive the Bretschneider's Formula.

Inequalities [edit]

Area [edit]

If a convex quadrilateral has the sequent sides a, b, c, d and the diagonals p, q, then its surface area K satisfies^[37]

${\displaystyle K\leq {\tfrac {1}{4}}(a+c)(b+d)}$ with equality simply for a rectangle.

${\displaystyle K\leq {\tfrac {1}{four}}(a^{two}+b^{2}+c^{2}+d^{two})}$ with equality only for a square.

${\displaystyle K\leq {\tfrac {one}{four}}(p^{2}+q^{two})}$ with equality simply if the diagonals are perpendicular and equal.

${\displaystyle G\leq {\tfrac {1}{2}}{\sqrt {(a^{two}+c^{2})(b^{two}+d^{ii})}}}$ with equality but for a rectangle.^[16]

From Bretschneider'due south formula information technology directly follows that the area of a quadrilateral satisfies

${\displaystyle K\leq {\sqrt {(s-a)(due south-b)(s-c)(s-d)}}}$

with equality if and only if the quadrilateral is cyclic or degenerate such that one side is equal to the sum of the other three (it has collapsed into a line segment, then the area is cipher).

The area of any quadrilateral also satisfies the inequality^[38]

${\displaystyle \displaystyle Chiliad\leq {\tfrac {ane}{2}}{\sqrt[{3}]{(ab+cd)(air conditioning+bd)(advertisement+bc)}}.}$

Denoting the perimeter as L, nosotros have^{[38] : p.114}

${\displaystyle K\leq {\tfrac {1}{sixteen}}Fifty^{2},}$

with equality only in the case of a foursquare.

The area of a convex quadrilateral as well satisfies

${\displaystyle K\leq {\tfrac {1}{2}}pq}$

for diagonal lengths p and q, with equality if and simply if the diagonals are perpendicular.

Let a, b, c, d be the lengths of the sides of a convex quadrilateral ABCD with the area 1000 and diagonals Air conditioning = p, BD = q. And so^[39]

${\displaystyle Yard\leq {\frac {a^{2}+b^{2}+c^{ii}+d^{2}+p^{ii}+q^{2}+pq-air conditioning-bd}{8}}}$ with equality only for a square.

Let a, b, c, d be the lengths of the sides of a convex quadrilateral ABCD with the surface area Chiliad, and then the following inequality holds:^[40]

${\displaystyle K\leq {\frac {1}{3+{\sqrt {three}}}}(ab+ac+ad+bc+bd+cd)-{\frac {one}{2(ane+{\sqrt {3}})^{2}}}(a^{2}+b^{2}+c^{2}+d^{two})}$ with equality only for a square.

Diagonals and bimedians [edit]

A corollary to Euler's quadrilateral theorem is the inequality

${\displaystyle a^{ii}+b^{two}+c^{2}+d^{two}\geq p^{two}+q^{2}}$

where equality holds if and simply if the quadrilateral is a parallelogram.

Euler also generalized Ptolemy'south theorem, which is an equality in a circadian quadrilateral, into an inequality for a convex quadrilateral. It states that

${\displaystyle pq\leq ac+bd}$

where there is equality if and only if the quadrilateral is cyclic.^{[24] : p.128–129} This is ofttimes called Ptolemy's inequality.

In any convex quadrilateral the bimedians m, n and the diagonals p, q are related past the inequality

${\displaystyle pq\leq one thousand^{ii}+northward^{2},}$

with equality belongings if and only if the diagonals are equal.^{[41] : Prop.1} This follows directly from the quadrilateral identity ${\displaystyle chiliad^{ii}+northward^{2}={\tfrac {ane}{2}}(p^{2}+q^{2}).}$

Sides [edit]

The sides a, b, c, and d of any quadrilateral satisfy^{[42] : p.228, #275}

${\displaystyle a^{2}+b^{ii}+c^{two}>{\frac {d^{2}}{3}}}$

and^{[42] : p.234, #466}

${\displaystyle a^{iv}+b^{4}+c^{4}\geq {\frac {d^{four}}{27}}.}$

Maximum and minimum backdrop [edit]

Among all quadrilaterals with a given perimeter, the one with the largest surface area is the square. This is chosen the isoperimetric theorem for quadrilaterals. It is a directly upshot of the surface area inequality^{[38] : p.114}

${\displaystyle K\leq {\tfrac {1}{16}}Fifty^{2}}$

where Yard is the area of a convex quadrilateral with perimeter L. Equality holds if and only if the quadrilateral is a foursquare. The dual theorem states that of all quadrilaterals with a given surface area, the square has the shortest perimeter.

The quadrilateral with given side lengths that has the maximum area is the cyclic quadrilateral.^[43]

Of all convex quadrilaterals with given diagonals, the orthodiagonal quadrilateral has the largest area.^{[38] : p.119} This is a direct consequence of the fact that the area of a convex quadrilateral satisfies

${\displaystyle Yard={\tfrac {1}{2}}pq\sin {\theta }\leq {\tfrac {1}{ii}}pq,}$

where θ is the angle between the diagonals p and q. Equality holds if and only if θ = 90°.

If P is an interior point in a convex quadrilateral ABCD, so

${\displaystyle AP+BP+CP+DP\geq AC+BD.}$

From this inequality it follows that the point inside a quadrilateral that minimizes the sum of distances to the vertices is the intersection of the diagonals. Hence that indicate is the Fermat point of a convex quadrilateral.^{[44] : p.120}

Remarkable points and lines in a convex quadrilateral [edit]

The centre of a quadrilateral can exist defined in several different ways. The "vertex centroid" comes from because the quadrilateral as beingness empty but having equal masses at its vertices. The "side centroid" comes from considering the sides to take constant mass per unit length. The usual centre, chosen simply centroid (centre of area) comes from considering the surface of the quadrilateral as having constant density. These three points are in general not all the same point.^[45]

The "vertex centroid" is the intersection of the two bimedians.^[46] As with any polygon, the x and y coordinates of the vertex centroid are the arithmetics means of the x and y coordinates of the vertices.

The "area centroid" of quadrilateral ABCD can exist constructed in the following way. Let Thou_a , G_b , Grand_c , Thousand_d be the centroids of triangles BCD, ACD, ABD, ABC respectively. Then the "expanse centroid" is the intersection of the lines Thou_aChiliad_c and 1000_bOne thousand_d .^[47]

In a general convex quadrilateral ABCD, there are no natural analogies to the circumcenter and orthocenter of a triangle. But two such points tin can be constructed in the following way. Allow O_a , O_b , O_c , O_d exist the circumcenters of triangles BCD, ACD, ABD, ABC respectively; and denote by H_a , H_b , H_c , H_d the orthocenters in the same triangles. So the intersection of the lines O_aO_c and O_bO_d is called the quasicircumcenter, and the intersection of the lines H_aH_c and H_bH_d is called the quasiorthocenter of the convex quadrilateral.^[47] These points tin can be used to ascertain an Euler line of a quadrilateral. In a convex quadrilateral, the quasiorthocenter H, the "area centroid" Chiliad, and the quasicircumcenter O are collinear in this club, and HG = 2GO.^[47]

There can besides be defined a quasinine-betoken middle E equally the intersection of the lines E_aEast_c and E_bE_d , where E_a , East_b , E_c , East_d are the 9-point centers of triangles BCD, ACD, ABD, ABC respectively. Then E is the midpoint of OH.^[47]

Some other remarkable line in a convex non-parallelogram quadrilateral is the Newton line, which connects the midpoints of the diagonals, the segment connecting these points beingness bisected by the vertex centroid. One more interesting line (in some sense dual to the Newton's i) is the line connecting the point of intersection of diagonals with the vertex centroid. The line is remarkable by the fact that it contains the (area) centroid. The vertex centroid divides the segment connecting the intersection of diagonals and the (area) centroid in the ratio 3:one.^[48]

For any quadrilateral ABCD with points P and Q the intersections of AD and BC and AB and CD, respectively, the circles (PAB), (PCD), (QAD), and (QBC) pass through a mutual bespeak M, called a Miquel point.^[49]

For a convex quadrilateral ABCD in which E is the bespeak of intersection of the diagonals and F is the point of intersection of the extensions of sides BC and Advertising, allow ω be a circumvolve through Eastward and F which meets CB internally at K and DA internally at N. Let CA meet ω again at Fifty and let DB meet ω again at K. Then there holds: the straight lines NK and ML intersect at indicate P that is located on the side AB; the direct lines NL and KM intersect at point Q that is located on the side CD. Points P and Q are called "Pascal points" formed by circle ω on sides AB and CD. ^{[50] [51] [52]}

Other backdrop of convex quadrilaterals [edit]

• Allow exterior squares be drawn on all sides of a quadrilateral. The segments connecting the centers of opposite squares are (a) equal in length, and (b) perpendicular. Thus these centers are the vertices of an orthodiagonal quadrilateral. This is called Van Aubel's theorem.
• For any uncomplicated quadrilateral with given edge lengths, there is a cyclic quadrilateral with the aforementioned edge lengths.^[43]
• The four smaller triangles formed past the diagonals and sides of a convex quadrilateral have the property that the product of the areas of two opposite triangles equals the product of the areas of the other two triangles.^[53]

Taxonomy [edit]

A hierarchical taxonomy of quadrilaterals is illustrated past the figure to the correct. Lower classes are special cases of college classes they are connected to. Annotation that "trapezoid" here is referring to the North American definition (the British equivalent is a trapezium). Inclusive definitions are used throughout.

Skew quadrilaterals [edit]

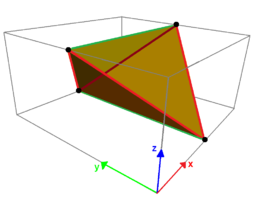
A non-planar quadrilateral is called a skew quadrilateral. Formulas to compute its dihedral angles from the edge lengths and the angle between two adjacent edges were derived for work on the backdrop of molecules such as cyclobutane that incorporate a "puckered" band of 4 atoms.^[54] Historically the term gauche quadrilateral was as well used to mean a skew quadrilateral.^[55] A skew quadrilateral together with its diagonals form a (possibly non-regular) tetrahedron, and conversely every skew quadrilateral comes from a tetrahedron where a pair of reverse edges is removed.

Encounter besides [edit]

• Complete quadrangle
• Perpendicular bisector construction of a quadrilateral
• Saccheri quadrilateral
• Types of mesh § Quadrilateral
• Quadrangle (geography)

References [edit]

1. ^ ^{a b c} "Quadrilaterals - Foursquare, Rectangle, Rhombus, Trapezoid, Parallelogram". Mathsisfun.com . Retrieved 2020-09-02 .
2. ^ "Sum of Angles in a Polygon". Cuemath . Retrieved 22 June 2022.
3. ^ Martin, George Edward (1982), Transformation geometry, Undergraduate Texts in Mathematics, Springer-Verlag, Theorem 12.1, page 120, doi:10.1007/978-1-4612-5680-9, ISBN0-387-90636-3, MR 0718119
4. ^ "Archived copy" (PDF). Archived from the original (PDF) on May 14, 2014. Retrieved June twenty, 2013. {{cite web}}: CS1 maint: archived copy as championship (link)
5. ^ "Rectangles Calculator". Cleavebooks.co.uk . Retrieved 1 March 2022.
6. ^ Keady, 1000.; Scales, P.; Németh, S. Z. (2004). "Watt Linkages and Quadrilaterals". The Mathematical Gazette. 88 (513): 475–492. doi:10.1017/S0025557200176107. S2CID 125102050.
7. ^ Jobbings, A. K. (1997). "Quadric Quadrilaterals". The Mathematical Gazette. 81 (491): 220–224. doi:10.2307/3619199. JSTOR 3619199. S2CID 250440553.
8. ^ Beauregard, R. A. (2009). "Diametric Quadrilaterals with 2 Equal Sides". College Mathematics Journal. 40 (1): 17–21. doi:10.1080/07468342.2009.11922331. S2CID 122206817.
9. ^ Hartshorne, R. (2005). Geometry: Euclid and Beyond. Springer. pp. 429–430. ISBN978-one-4419-3145-0.
10. ^ "Stars: A Second Look" (PDF). Mysite.mweb.co.za. Archived from the original (PDF) on March 3, 2016. Retrieved March 1, 2022.
11. ^ Butler, David (2016-04-06). "The crossed trapezium". Making Your Own Sense . Retrieved 2017-09-13 .
12. ^ Eastward.W. Weisstein. "Bimedian". MathWorld – A Wolfram Spider web Resource.
13. ^ E.Westward. Weisstein. "Maltitude". MathWorld – A Wolfram Spider web Resource.
14. ^ ^{a b c d} Weisstein, Eric W. "Quadrilateral". mathworld.wolfram.com . Retrieved 2020-09-02 .
15. ^ Harries, J. "Area of a quadrilateral," Mathematical Gazette 86, July 2002, 310–311.
16. ^ ^{a b c} Josefsson, Martin (2013), "Five Proofs of an Area Characterization of Rectangles" (PDF), Forum Geometricorum, 13: 17–21 .
17. ^ R. A. Johnson, Advanced Euclidean Geometry, 2007, Dover Publ., p. 82.
18. ^ Mitchell, Douglas W., "The expanse of a quadrilateral," Mathematical Gazette 93, July 2009, 306–309.
19. ^ https://world wide web.mathcentre.air-conditioning.uk/resources/uploaded/mc-ty-triangleformulae-2009-ane.pdf^{[ blank URL PDF ]}
20. ^ J. L. Coolidge, "A historically interesting formula for the expanse of a quadrilateral", American Mathematical Monthly, 46 (1939) 345–347.
21. ^ Due east.W. Weisstein. "Bretschneider'south formula". MathWorld – A Wolfram Web Resource.
22. ^ Archibald, R. C., "The Area of a Quadrilateral", American Mathematical Monthly, 29 (1922) pp. 29–36.
23. ^ ^{a b} Josefsson, Martin (2011), "The Expanse of a Bicentric Quadrilateral" (PDF), Forum Geometricorum, eleven: 155–164 .
24. ^ ^{a b c d e f} Altshiller-Court, Nathan, Higher Geometry, Dover Publ., 2007.
25. ^ ^{a b} Josefsson, Martin (2016) '100.31 Heron-similar formulas for quadrilaterals', The Mathematical Gazette, 100 (549), pp. 505–508.
26. ^ "Diagonals of Quadrilaterals -- Perpendicular, Bisecting or Both". Math.okstate.edu . Retrieved ane March 2022.
27. ^ Rashid, Chiliad. A. & Ajibade, A. O., "Ii conditions for a quadrilateral to be circadian expressed in terms of the lengths of its sides", Int. J. Math. Educ. Sci. Technol., vol. 34 (2003) no. five, pp. 739–799.
28. ^ Andreescu, Titu & Andrica, Dorian, Complex Numbers from A to...Z, Birkhäuser, 2006, pp. 207–209.
29. ^ ^{a b} Josefsson, Martin (2012), "Characterizations of Orthodiagonal Quadrilaterals" (PDF), Forum Geometricorum, 12: 13–25 .
30. ^ Hoehn, Larry (2011), "A New Formula Concerning the Diagonals and Sides of a Quadrilateral" (PDF), Forum Geometricorum, eleven: 211–212 .
31. ^ Leversha, Gerry, "A property of the diagonals of a cyclic quadrilateral", Mathematical Gazette 93, March 2009, 116–118.
32. ^ H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, MAA, 1967, pp. 52–53.
33. ^ "Mateescu Constantin, Respond to Inequality Of Diagonal".
34. ^ C. V. Durell & A. Robson, Advanced Trigonometry, Dover, 2003, p. 267.
35. ^ "Original Bug Proposed by Stanley Rabinowitz 1963–2005" (PDF). Mathpropress.com . Retrieved March i, 2022.
36. ^ "E. A. José García, Two Identities and their Consequences, MATINF, six (2020) 5-11". Matinf.upit.ro . Retrieved 1 March 2022.
37. ^ O. Bottema, Geometric Inequalities, Wolters–Noordhoff Publishing, The Netherlands, 1969, pp. 129, 132.
38. ^ ^{a b c d} Alsina, Claudi; Nelsen, Roger (2009), When Less is More than: Visualizing Basic Inequalities, Mathematical Association of America, p. 68 .
39. ^ Dao Thanh Oai, Leonard Giugiuc, Problem 12033, American Mathematical Monthly, March 2018, p. 277
40. ^ Leonard Mihai Giugiuc; Dao Thanh Oai; Kadir Altintas (2018). "An inequality related to the lengths and area of a convex quadrilateral" (PDF). International Periodical of Geometry. vii: 81–86.
41. ^ Josefsson, Martin (2014). "Properties of equidiagonal quadrilaterals". Forum Geometricorum. 14: 129–144.
42. ^ ^{a b} "Inequalities proposed in Crux Mathematicorum (from vol. 1, no. 1 to vol. 4, no. 2 known as "Eureka")" (PDF). Imomath.com . Retrieved March one, 2022.
43. ^ ^{a b} Peter, Thomas, "Maximizing the Expanse of a Quadrilateral", The College Mathematics Journal, Vol. 34, No. four (September 2003), pp. 315–316.
44. ^ Alsina, Claudi; Nelsen, Roger (2010). Charming Proofs : A Journey Into Elegant Mathematics. Mathematical Association of America. pp. 114, 119, 120, 261. ISBN978-0-88385-348-ane.
45. ^ "Two Centers of Mass of a Quadrilateral". Sites.math.washington.edu . Retrieved 1 March 2022.
46. ^ Honsberger, Ross, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Math. Assoc. Amer., 1995, pp. 35–41.
47. ^ ^{a b c d} Myakishev, Alexei (2006), "On 2 Remarkable Lines Related to a Quadrilateral" (PDF), Forum Geometricorum, half dozen: 289–295 .
48. ^ John Boris Miller. "Centroid of a quadrilateral" (PDF). Austmd.org.au . Retrieved March i, 2022.
49. ^ Chen, Evan (2016). Euclidean Geometry in Mathematical Olympiads. Washington, D.C.: Mathematical Clan of America. p. 198. ISBN9780883858394.
50. ^ David, Fraivert (2019), "Pascal-points quadrilaterals inscribed in a cyclic quadrilateral", The Mathematical Gazette, 103 (557): 233–239, doi:10.1017/magazine.2019.54, S2CID 233360695 .
51. ^ David, Fraivert (2019), "A Set of Rectangles Inscribed in an Orthodiagonal Quadrilateral and Divers by Pascal-Points Circles", Journal for Geometry and Graphics, 23: 5–27 .
52. ^ David, Fraivert (2017), "Properties of a Pascal points circumvolve in a quadrilateral with perpendicular diagonals" (PDF), Forum Geometricorum, 17: 509–526 .
53. ^ Josefsson, Martin (2013). "Characterizations of Trapezoids" (PDF). Forum Geometricorum. 13: 23–35.
54. ^ Barnett, K. P.; Capitani, J. F. (2006). "Modular chemical geometry and symbolic adding". International Journal of Breakthrough Chemistry. 106 (ane): 215–227. Bibcode:2006IJQC..106..215B. doi:10.1002/qua.20807.
55. ^ Hamilton, William Rowan (1850). "On Some Results Obtained by the Quaternion Analysis Respecting the Inscription of "Gauche" Polygons in Surfaces of the Second Guild" (PDF). Proceedings of the Royal Irish University. 4: 380–387.

External links [edit]

Wikimedia Commons has media related to Tetragons.

• "Quadrangle, complete", Encyclopedia of Mathematics, EMS Printing, 2001 [1994]
• Quadrilaterals Formed by Perpendicular Bisectors, Projective Collinearity and Interactive Classification of Quadrilaterals from cut-the-knot
• Definitions and examples of quadrilaterals and Definition and properties of tetragons from Mathopenref
• A (dynamic) Hierarchical Quadrilateral Tree at Dynamic Geometry Sketches
• An extended nomenclature of quadrilaterals Archived 2019-12-30 at the Wayback Auto at Dynamic Math Learning Homepage Archived 2018-08-25 at the Wayback Machine
• The role and function of a hierarchical classification of quadrilaterals by Michael de Villiers

Which Quadrilaterals Have Perpendicular Diagonals,

Source: https://en.wikipedia.org/wiki/Quadrilateral

Posted by: brownpiten2002.blogspot.com

Share this post